Gradient Descent
Find the treasure hidden in the deepest point of the ocean floor by lowering a probe from your research ship. Use the arrow buttons to move the ship and the circle button to send the probe. After you find it, read on and discover how AIs learn through the same strategies you developed to win.
After playing a couple of times you probably figured out that the quickest way to find the deepest point in the ocean floor is by paying attention to the slope found by the probe: how steep the floor was at that point and in which direction it was inclined. Although you can’t see the bottom and don’t have a full picture of what it looks like, the slope suggests where to continue your search.
The best treasure searching strategy is the same that artificial neural networks use to learn: an algorithm called (just like our game) gradient descent.
In our Piano Genie and Neural Numbers trails we talked about how neural networks learn through examples. We give the network an example, it produces an output, we analyze how good or bad it was and provide feedback to the network. The network corrects its response and we try again.
Let’s zoom in on the process. After the network produces the output, we measure how far it was from the desired result, and we call this amount “error”. The neural network gets better at its task by adjusting the strength of the connections between its artificial neurons in a way that makes the error as small as possible for all possible inputs. Every step of the training process (enter input, check output, measure error, adjust) takes some time, and we need to repeat it thousands or millions of times, so the fastest way to minimize the error has to be used. Just like you, the network uses the slope to decide how to adjust its connections and try again.
Local minimum
One of the difficulties in searching for treasure is also a problem when we’re training an AI. If you’re lucky by following along the ocean floor you reach its lowest point. If you’re not so lucky you reach a point that’s separated by one or more “hills” from the actual deepest point. A valley, but not the deepest one. We call this a “local minimum”.
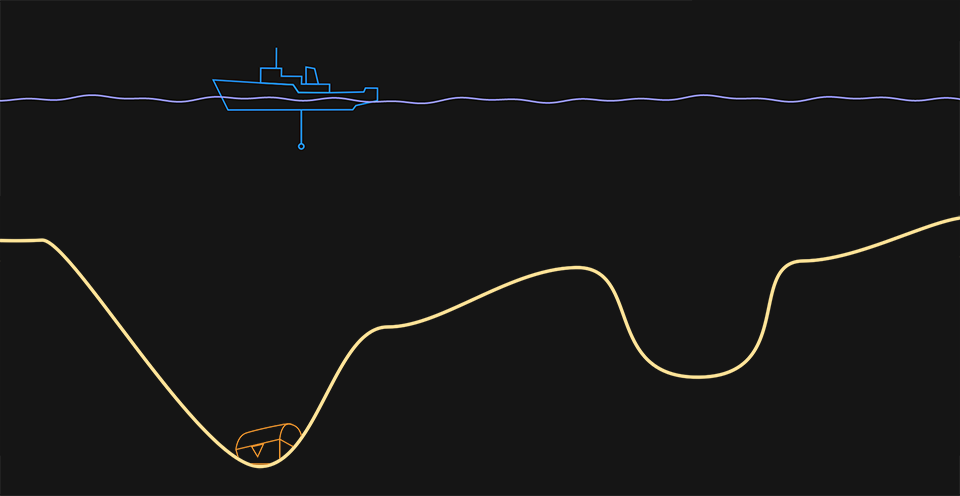
If you start searching over the left side of the screen you’ll find the deepest point, where the treasure is. If you start searching over the right side you might find the local minimum instead.
When a neural network finds a local minimum it gets stuck in its learning process. It made little adjustments to its connections by following the slope, getting better and better at its task. Now its performance has reached a plateau, and any adjustment leads to equal or worse results. It might be more disheartening even: In the real world there are no guarantees that the neural network built will be able to solve the task as well as expected. Was the treasure a lie?
The strategy for getting out of a local minimum is about the same as you might use in the game: try something different, pick a new starting point and search again. AIs sometimes need this kind of adventurous spirit to explore randomly in combination with the efficient and systematic approach of the gradient descent. The space they’re searching can be really rocky, full of ups and downs, and this might not be easy to notice by sending just a few “probes”.
We’re going to need a bigger boat
There is one big difference between our game and the search to minimize error that neural networks make. Our boat can only move right or left because the game is 2D (it moves in one dimension, it probes in another). You can probably imagine how this would work in 3D in the real world: the boat could move in two dimensions (north / south and east / west) and probe in the third. The ocean floor in our three dimensional world is not a simple curve, but a surface with hills and valleys, but the slope can still be followed (imagine how a ball would roll down) to reach the lowest point or a local minimum.
Neural networks search for the deepest point in an ocean with thousands of dimensions. It’s impossible to draw or visualize it, but we can still think about it. With a real ship you could say “let’s search 1 mile north and 2 miles east from the last point” to indicate how to move over two dimensions; for a thousand dimensions you just provide a thousand individual numbers. The mathematics stay the same and make it possible to calculate the slope. We can follow the exact same procedure, with the same problems as the simple 2D case.
You can probably imagine why AI requires really fast computers that might train a neural network for days, weeks or longer, even with the most efficient search strategy.
Some things to think about
This process of making adjustments to optimize results and having strategies to get out of a local minimum has many parallels in real life. Pro athletes sometimes change their technique to reach better results (golfer Tiger Woods changed his swing a couple of times during his career, without guarantees it’d lead to improvements). Established professional singers sometimes require coaching to change their vocal technique and avoid vocal cord damage. Populations of animals sometimes take the risky decision to migrate to find more food or a better environment. You could even use this strategy to find the perfect combination of ice cream flavors.
- Can you think of other ways in which the learning process of AIs is similar to how living beings make intelligent decisions?
- Risk taking and randomness are sometimes associated with irrationality, how can we understand and accept them as a necessary part of intelligent decision making?
In the I AM A.I. Exhibition
You can play Gradient Descent in our exhibition. You can also continue learning how AI’s think with our Sumory and Reinforcement Learning exhibits.
Learn how to visit.
Text is available under the Creative Commons Attribution License.